Parallel transport
Before all, see relationship parallel transport, covariant derivatives and metrics.
Intuitive approach
The following intuitions are about the transport corresponding to an existent metric in a surface (inherited or not from that of $\mathbb{R}^3$), that is, the Levi-Civita parallel transport.
Extrinsic construction
Suppose the metric has a surface inherited from that of $\mathbb{R}^3$. To parallel transport a vector $w$ along a curve $K$ in a surface $S$ we break $K$ into small steps of length $\epsilon$. In every step we translate $w$ from one point $p$ to the next one $q$, according to our knowledge of the parallelism of $\mathbb{R}^3$. Since the translated vector is no longer tangent to $S$, we project it to $T_qS$ by means of
$$ w_q:=w-(w\cdot n_q)n_q $$where $n_q$ is the unit normal at $q$. This is only an approximation, of course.
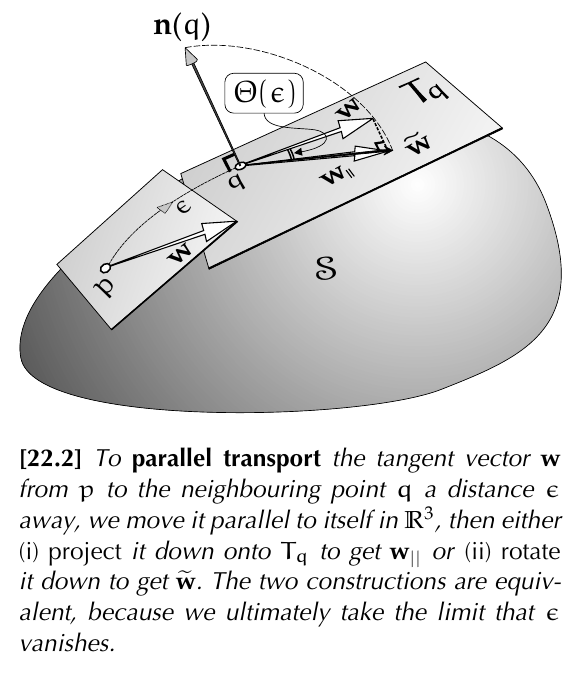
The given vector doesn't have to be initially tangent to the curve $K$. If this is the case, the parallel transported vector doesn't have to remain tangent to the curve $K$. This happens when the curve is a geodesic.
Another way to construct the parallel transport (@needham2021visual page 237):

Intrinsic construction
(@needham2021visual page 283)
It takes into account parallel transport along a geodesic $G$ (if the curve is not a geodesic, we break it down into geodesic segments). To achieve parallel transport along $G$, it is only necessary to keep the angle with the tangent vector of $G$ constant (and the length).
Constancy of angles
From this last intuition can be concluded that if two vectors are parallel transported along a curve on a surface then the angle between them remains constant. That it, parallel transport preserve the angles.
Keep an eye: the parallel transport of $v$ along a curve $\gamma$ doesn't preserve the angle between $v$ and $\dot{\gamma}$, unless $\dot{\gamma}$ is a parallel transported vector field, i.e., $\gamma$ is a geodesic!
Covariant derivative
Still from the intuitive point of view, a defined notion of parallel transport on a surface leads to an idea of covariant derivative operator on this surface. Suppose that we know how to parallel transport vectors along curves, and fixed a curve $K$ with tangent vector $v$ at $p=K(0)$, denote by $\xi_{\parallel}(q\to p)$ the parallel transport of $\xi \in T_q S$ to $T_pS$, then, for a vector field $w$ on the surface, we defined
$$ (\nabla_v w)_p=\lim_{\epsilon \to 0} \dfrac{w(q_{\epsilon})_{\parallel}(q_{\epsilon}\to p)-w(p)}{\epsilon} $$where $q_{\epsilon}=K(\epsilon)$.
Conversely, this covariant derivative, if given a priori, let us recover the parallel transport. See this construction.
Formal approach
Construction from a covariant derivative operator
Suppose a manifold $M$ with a covariant derivative operator $\nabla$ defined on it. A vector field $X$ on $M$ is constant along a curve $c$ ($X$ is a parallel vector field along $c$) in $M$ if
$$ \nabla_{c'(t)} X=0 $$This is well defined since covariant derivative only depends on the value at a point in the first vector field (see linear connection#Definition as operator).
If the vector field $X(t)$ is only defined along the curve $c$, we consider the covariant derivative along a curve $D_c$. With this in mind we can say when a vector field defined along a curve $c$ is constant along the curve: $D_c X=0$ for every $c(t)$.
In @malament2012topics page 57 it is also shown that
Proposition
Given a manifold $(M,\nabla)$ and a curve $c$ on it, and a vector $v$ at a point $p=c(0)$, there exists a unique vector field $X(t)$ along $c$ that is constant along the curve and such that $X(p)=v$. This vector field is called the parallel transport of $v$ along $c$. $\blacksquare$
Definition of parallel transport
I suppose that parallel transport can be defined in abstract, and then it must be possible to prove that it gives rise to a covariant derivative operator (the converse of the previous section). See section "covariant derivative" in parallel transport#Intuitive approach above.
Properties
- If the space has curvature then parallel transport depends on the path chosen to transport. This is called holonomy.
- For the "gap" of a parallelogram made of parallel transported vectors see torsion of a connection.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: